/Ixx Ixy Ixz\ Ixx = S(mi(yi²+zi²)), x, y, z zyklisch
I = |Iyx Iyy Iyz| (1)
\Izx Izy Izz/ Ixy = S(mi xi yi), x, y, z zyklisch
Dabei bedeuten mi die Masse des i-ten Atoms und xi,
yi und zi dessen Koordinaten. Der Summationsindex i
läuft über alle Atome des Moleküls. Die Größen
Igg nennt man Trägheitsmomente, die Größen
Igg' (g¹g') heißen Deviationsmomente. Wie man aus der
Definition der Deviationsmomente sehen kann, ist der Trägheitstensor
symmetrisch, d.h. Ixy = Iyx usw. Durch geeignete Wahl
des Koordinatensystems kann man erreichen, daß alle Deviationsmomente
verschwinden und der Trägheitstensor diagonal wird. Dieses
Koordinatensystem wird dann als das Hauptträgheitssystem des
Moleküls bezeichnet. Die Elemente des Hauptträgheitstensors sind
die drei Hauptträgheitsmomente Ix = Ixx,
Iy = Iyy und Iz = Izz. Diese drei Hauptträgheitsmomente werden nun ihrer Größe nach als Ia, Ib und Ic benannt, wobei gilt: Ia < Ib < Ic. Sind alle drei Hauptträgheitsmomente verschieden, so spricht man von einem asymmetrischen Kreisel. Sind zwei der drei Haupträgheitsmomente gleich, so nennt man diese Moleküle symmetrische Kreisel. Je nachdem, welche der beiden Hauptträgheitsmomente gleich sind, wird weiter unterschieden in langgestreckte (prolate) Kreisel (Ia < Ib = Ic) und abgeplattete (oblate) Kreisel (Ia = Ib < Ic). Ein Molekül mit drei gleichen Hauptträgheitsmomenten bezeichnet man als Kugelkreisel.
A = h/(8p²Ia) , (entsprechend für B und C), (2)wobei h das Plancksche Wirkungsquantum darstellt. Der Faktor h/8p²wird oft als Umrechnungsfaktor von Rotationskonstanten in Trägheitsmomente und umgekehrt verwendet. Der aktuelle Wert beträgt 505379,1(6) MHz u Ų.
Der Hamiltonoperator, der die Rotation eines asymmetrischen Kreisels beschreibt, kann wie folgt formuliert werden:
H = (4·pi²)/h (A·Pa² B·Pb² C·Pc²) . (3)Dabei sind die Pg die Drehimpulsoperatoren bezüglich der drei Hauptträgheitsachsen. Die Berechnung der Energieniveaus wird erleichtert, wenn man den Hamiltonoperator, wie von Ray [14] vorgeschlagen, etwas umformuliert:
H = (4·p²)/h (1/2 (A+C)P² + 1/2 (A-C) H(k)) . (4)Mit P² = Pa² + Pb² + Pc². H(k) ist der reduzierte Hamiltonoperator. Er ist definiert als:
H(k) = Pa² + kPb² - Pc² . (5)k ist der Raysche Asymmetrieparameter für den gilt:
k = (2 B - A - C)/(A - C) . (6)Dieser Parameter ist gleichsam ein Maß für die Asymmetrie des Trägheitsellipsoids und wird für die beiden symmetrischen Grenzfälle +1 (oblate) bzw. -1 (prolate).
Für die Energie eines Rotationsniveaus eines starren Rotators erhält man dann:
E = h (½(A+C)J(J+1) + ½(A-C)EJt(k)) . (7)Dabei ist t eine Laufzahl, welche zur Identifizierung der einzelnen Niveaus verwendet wird. Früher wurden zur Berechnung der Energieniveaus oft die tabellierten Eigenwerte EJt(k) von H(k) benutzt, während man heute aufgrund der Verfügbarkeit schneller Rechner H(k) numerisch diagonalisieren kann und dadurch genauere Ergebnisse erhält als durch Interpolation der Tabellenwerte.
Für die Zentrifugalverzerrungskorrekturen nach Watson gibt es zwei Möglichkeiten: die S-Reduktion (für Moleküle nahe dem symmetrischem Grenzfall) und die A-Reduktion (allgemein für asymmetrische Kreisel). Im Falle des Dimethylcyclohexadienons, das ein fast symmetrisches Trägheitsellipsoid besitzt, wurden beide Reduktionen verwendet. Die Standardabweichung der Anpassung war in beiden Fällen gleich, die Parameter waren aber in der S-Reduktion etwas stärker korreliert, sodaß (auch zur besseren Vergleichbarkeit der Ergebnisse in dieser Arbeit) nur die Konstanten der A-Reduktion angegeben werden.
Die Zeitskala der Kernschwingungen ist so kurz, daß mit den meisten spektroskopischen Methoden, die zur Strukturbestimmung angewandt werden, keine zeitliche Auflösung der Kernbewegung erfolgen kann. So erhält man also nur den Erwartungswert der entsprechenden Meßgröße über der Wellenfunktion des Schwingungszustandes. Bei der Elektronenbeugung sind die Wechselwirkungszeiten zwar so kurz, daß gleichsam "Momentaufnahmen" der Kernabstände gemacht werden. Zum Erzeugen des Beugungsbildes sind jedoch viele einzelne Elektronen nötig, die alle möglichen verschiedenen Kernabstände "abbilden" und so wiederum zu einer Mittelung führen.
Da im Normalfall mehr als ein Schwingungsniveau besetzt ist, wird die Struktur, die man experimentell bestimmt, ganz entscheidend davon abhängen, ob man experimentell nur einen Schwingungszustand erfaßt oder mehrere. Im letzteren Fall ist auch noch von Bedeutung, wie die Mittelung über die Schwingungszustände erfolgt. All diese Faktoren sind stark von der verwendeten Methode abhängig. So erhält man zum Beispiel in der Mikrowellenspektroskopie Strukturdaten für einen bestimmten Schwingungszustand, während in der Gasphasen-Elektronenbeugung über alle besetzten Schwingungszustände gemittelt wird.
Ig,0 = h/(8p² Bg,0) , g = a, b, c. (2a)Dabei ist Bg,0 die Rotationskonstante im Schwingungsgrundzustand bezüglich der Achse g (für Ba,0 wird meistens A0 geschrieben, entsprechend B0 und C0 für die b- und c-Achsen) und Ig,0 das Hauptträgheitsmoment im Schwingungsgrundzustand bezüglich der Achse g. Werden Größen ohne Index angegeben, so beziehen sich die Werte i.a. auf den Schwingungsgrundzustand.
Aus den Hauptträgheitsmomenten ist dann prinzipiell die Struktur zugänglich, denn es gilt:
Ia,0 = S(mi (b0,i² + c0,i²) , a, b, c zyklisch, (8)Hier steht mi für die Masse des i-ten Atoms und g0,i für den Erwartungswert der g-Koordinate des i-ten Atoms im Schwingungsgrundzustand. Der Summationsindex i läuft über alle Atome.
Durch die Messung eines bestimmten Isotopomers erhält man maximal drei unabhängige Hauptträgheitsmomente (bei planaren und linearen Molekülen und bei symmetrischen Kreiseln sogar weniger). Vor allem bei größeren Molekülen ist die Anzahl der unabhängigen Strukturparameter jedoch meist erheblich größer. In solchen Fällen muß man entweder Annahmen über bestimmte Strukturparameter machen oder zusätzliche Informationen aus der Messung isotopensubstituierter Moleküle heranziehen. Bei dem zweiten Verfahren muß vorausgesetzt werden, daß sich die Geometrie des Moleküls zwischen zwei Isotopomeren nicht unterscheidet. Für die "Ruhepositionen" (die re-Struktur) trifft dies zu. Die Wellenfunktionen - und damit auch die Erwartungswerte der Koordinaten - im schwingenden Molekül sind jedoch von der Masse abhängig. Besonders drastisch ist dieser Effekt verständlicherweise für Wasserstoffatome. Hier vergrößert sich die Masse bei Substitution durch Deuterium auf das Doppelte und diese Näherung ist dann offensichtlich ungenau.
Doch auch bei schwereren Atomen macht sich dieser Effekt außerhalb der experimentellen Fehlergrenzen bemerkbar und so ist eine r0-Struktur immer davon abhängig, welche Atome im Molekül für die Strukturbestimmung isotopiert wurden. Ein eindrückliches Beispiel hierfür ist Carbonylsulfid OCS. Die Struktur dieses Moleküls wird durch zwei unabhängige Strukturparameter beschrieben.
Da man aus
dem Mikrowellenspektrum dieses linearen Moleküls aber pro
Isotopenspezies nur ein Hauptträgheitsmoment erhält, muß man
mindestens zwei Isotopomere messen, um die Struktur bestimmen zu
können. Die Strukturdaten, die man für verschiedene Paare von
Isotopomeren erhält, sind in Tabelle B.1
zusammengefaßt.
Isotopomerenpaar r0(C=O) r0(C=S)
------------------------------------------
16O12C32S - 16O12C34S 1,1647 1,5576
16O12C32S - 16O13C32S 1,1629 1,5591
16O12C34S - 16O13C34S 1,1625 1,5594
16O12C32S - 18O12C32S 1,1552 1,5653
------------------------------------------
rmax - rmin 0,0095 0,0077
Tab. B.1: r0-Abstände für OCS aus unterschiedlichen
Isotopomeren-Paaren (aus [19]).
|a| = SQR(DPa/m(1+DPb/(Ia-Ib))(1+DPc/(Ia-Ic))),
a, b, c zyklisch. (9)
Dabei ist
DPa = -½(DIa-DIb-DIc) , a, b, c zyklisch, (10)mit
DIg = (I'g - Ig) , g = a, b, c (11)und
m = (M(M' - M))/(M + (M' - M). (12)M bedeutet dabei die Molekülmasse. Ungestrichene Größen beziehen sich auf das Muttermolekül, gestrichene Größen auf das isotopierte Molekül.
Wenn man alle nicht
symmetrie-äquivalenten Positionen isotopiert hat, erhält man aus
diesen Gleichungen also die Koordinaten aller Atome und kann daraus
Bindungsabstände und -winkel berechnen. Diese Struktur beschreibt dann
allerdings keines der gemessenen Spektren, sondern stellt gleichsam eine
Mittelung zwischen den verschiedenen r0-Strukturen dar.
Muttermolekül rs(C=O) rs(C=S)
--------------------------------------
16O12C32S 1,16012 1,56020
16O13C32S 1,16017 1,56008
16O12C34S 1,16075 1,55963
18O12C32S 1,15979 1,56063
--------------------------------------
rmax - rmin 0,00096 0,00100
Tab. B.2: rs-Abstände für OCS ausgehend von
unterschiedlichen Muttermolekülen (aus [21]).
Je nachdem, welches Isotopomer als Muttermolekül verwendet wird, erhält man zwar auch hier verschiedene Werte (vgl. Tab. B.2). Allerdings ist die Spannbreite der Werte deutlich kleiner. Während der Unterschied zwischen dem kürzesten und dem längsten C=O-Abstand bei der r0-Methode 0,0095 Å beträgt, so liegen die Extremwerte bei der rs-Methode nur etwa 10% dieses Betrages, nämlich 0,00096 Å, auseinander.
Bg,v = Bg,e - S(ag,i(vi + di/2)) , g = a, b, c. (13a) Bg,e = Bg,0 + ½ S(di ag,i) , g = a, b, c. (13b)Bg,v sind die Rotationskonstanten in dem Schwingungszustand, der durch den Satz v von 3N-6 Schwingungsquantenzahlen vi gekennzeichnet ist. Bg,e bezeichnet die Rotationskonstanten für den hypothetischen, schwingungslosen Zustand, di sind die Entartungsgrade der Normalschwingungen und ag,i sind die Rotations-Schwingungs-Wechselwirkungskonstanten. Der Summationsindex i läuft hierbei über alle 3N-6 Normalschwingungen, die in dem N-atomigen Molekül auftreten.
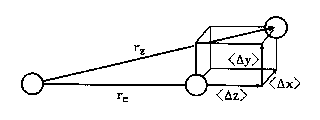
r²z= <r>0² = (re + <Dz>0)² + <Dx>²0 + <Dy>²0 (14a)
 |
| Abb. B.1: Veranschaulichung der verwendeten Größen. |
Dabei liegt die z-Achse jeweils in Kernverbindungsrichtung, die xund y-Achsen senkrecht dazu. Dz stellt die Abweichung in Kernverbindungsrichtung dar, während Dx und Dy senkrechte Schwingungsbeiträge wiedergeben.
Aus (14a) folgt:
rz = (re+<Dz>0)SQR(1+(<Dx>²0+<Dy>²0)/(re+<Dz>0)²) (14b)Eine Taylor-Entwicklung (SQR(1+x) » 1+x/2) liefert:
rz=(re+<Dz>0)(1+(<Dx>²0+<Dy>²0)/(2(re+<Dz>0)²))(15a) = re+<Dz>0+(<Dx>²0+<Dy>²0)/(2(re+<Dz>0) (15b)Die Erwartungswerte der senkrechten Schwingungsanteile sind typischerweise etwa 10-2 Å, ihre Quadrate also etwa 10-4 Å2. Da re meist zwischen 1 und 2 Å liegt trägt also der letzte Term in Gleichung (15b) i.a. weniger als 10-4 Å bei und kann vernachlässigt werden. So ist dann
rz » re + <Dz>0 , (16)Für eine harmonische Schwingung ist <Dz>0 Null und die Differenz zwischen re und rz resultiert nur aus anharmonischen Beiträgen. Korrigiert man die gemessenen Rotationskonstanten sowohl um harmonische als auch um anharmonische Beiträge, so erhält man Be-Konstanten. Berücksichtigt man jedoch nur den harmonischen Anteil, so erhält man die Bz-Konstanten*.(vgl. Gleichung (13b)) Kennt man also nur das harmonische Kraftfeld§, so kann man aus den Bg,0 die Bg,z berechnen, aus denen prinzipiell die rz-Struktur zugänglich ist:
Bg,z = Bg,0 + ½S(di·ag,iharm.) , g = a, b, c. (17)* Einige Autoren benutzen für die zugehörigen Trägheitsmomente I* anstatt Iz und für die Abstände <r> anstatt rz.
§ Diese Parameter sind physikalisch identisch mit den manchmal verwendeten re,h-Parametern.
Die so definierten Bindungslängen sind sehr ähnlich zu rz, jedoch mit zwei wichtigen Unterschieden: erstens erfolgt die Mittelung bei rz nur über einen Schwingungszustand, bei rg dagegen über alle, bei einer bestimmten Temperatur besetzten Zustände. Zweitens handelt es sich bei rg um mittlere Bindungslängen, bei rz jedoch um Abstände zwischen mittleren Atompositionen. Dementsprechend kommen in den entsprechenden Formeln nicht die Quadrate der Erwartungswerte vor, sondern die Erwartungswerte der Quadrate und man erhält ganz analog zu Gleichung (15b) oben:
rg»re+<Dz>+(<Dx²>+<Dy²>)/(2(re+<Dz)) (18a)Da <Dz> gegen re klein ist, kann man auch schreiben:
rg » re + <Dz> + (<Dx²> + <Dy²>)/2re (18b)Auch hier bedeutet Dz die Abweichung in Kernverbindungsrichtung, während Dx und Dy senkrechte Schwingungsbeiträge darstellen (vgl Abb. B.1). Während <Dx>² und <Dy>² ohne größere Fehler vernachlässigt werden können, stellen <Dx²> und <Dy²> bei genauen Messungen durchaus signifikante Größen dar.
Die rg-Abstände werden i.a. aus den ra-Abständen durch folgende Beziehung erhalten:
rg = ra + l²/ra. (19)Dabei ist l die zugehörige mittlere Schwingungsamplitude.
ra = re + <Dz> , (20)womit die Umwandlung von rg in ra gegeben ist durch
ra = rg - (<Dx²> + <Dy²>)/2re . (21)Die ra-Parameter stellen also um die senkrechten Anteile korrigierte rg-Parameter dar. Diese senkrechten Anteile weisen i.a. keine kubischen Anharmonizitäten auf*, und so kann man - wie bei der Umrechnung von r0-Parametern in rz-Parameter - nur mit Kenntnis des harmonischen Kraftfeldes eine ra-Struktur errechnen. Da hierbei nur die senkrechten Beiträge berücksichtigt werden, stellen die ra-Abstände gewissermaßen Abstände der Projektionen der Atome auf die Kernverbindungsachsen dar. Die ra-Parameter berücksichtigen also den sogenannten "shrinkage-effect" und ergeben - im Gegensatz zu den rg-Parametern - eine geometrisch konsistente Struktur, die vor allem die Bindungswinkel der Gleichgewichtsanordnung in guter Näherung beschreibt [18b].
* Meist sind die Potentiale für Schwingungen dieser Art in guter Näherung symmetrisch und weisen deshalb keine kubischen Anharmonizitäten auf. Die quartischen Terme sind meist schon so klein, daß man sie ohne größere Fehler vernachlässigen kann.
Die Tatsache, daß die Erwartungswerte, die in die ra-Struktur eingehen, Mittelungen über die Boltzmann-Verteilung bei einer gegebenen Temperatur widerspiegeln, macht eine Extrapolation auf den absoluten Nullpunkt wünschenswert, bei dem nur noch ein energetischer Zustand (der Schwingungsgrundzustand) besetzt ist. Eine solche Struktur nennt man ra0-Struktur. Sie ist physikalisch identisch mit der rz-Struktur*.
* Deshalb sind diese Parameter physikalisch identisch mit den re,h-Parametern.
Ic,e - Ia,e - Ib,e = 0. (22)Die Ig,e sind dabei die Hauptträgheitsmomente, die sich aus den Gleichgewichtspositionen der einzelnen Atome ergeben, und c stellt die Achse senkrecht zur Molekülebene dar*. Für ein reales, schwingendes Molekül gilt diese Beziehung jedoch nicht exakt. Vielmehr ist:
Ic,0 - Ia,0 - Ib,0 = D0. (23)Man nennt D0 Trägheitsdefekt. Für ebene Moleküle ist sein Betrag typischerweise kleiner als 0,2 uŲ. Zum Trägheitsdefekt tragen zwar auch Zentrifugalverzerrungseffekte und elektronische Anteile bei, diese sind jedoch im allgemeinen unbedeutend.
* Die Achse senkrecht zur Molekülebene ist bei planaren Molekülen immer die Achse mit dem größten Hauptträgheitsmoment.
Der Schwingungsanteil kann nochmals unterteilt werden in Beiträge von in-planeund out-of-plane-Schwingungen. Erstere sind üblicherweise positiv, letztere dagegen negativ und meist auch kleiner. Im Fall von tiefliegenden out-of-plane-Schwingungen überwiegt dagegen deren Einfluß und der Trägheitsdefekt ist negativ.
Die Größe und das Vorzeichen des Trägheitsdefektes stellen also ein wichtiges Kriterium für die Ebenheit eines Moleküls und die dominierenden Schwingungen dar.
Setzt man in Gleichung (23) die Definitionen für die Hauptträgheitsmomente ein, so findet man folgende Beziehung:
D0 = -2S(mi ci²) (24)Die Summe S(mi ci²) nennt man auch Planarmoment bezüglich der c-Achse Pc. Da es für nicht-ebene Moleküle nur bedingt sinnvoll ist, von einem Trägheitsdefekt zu sprechen, benutzt man hier im allgemeinen das Planarmoment. Aus diesem Planarmoment läßt sich bei Kenntnis der c-Koordinaten der Atome außerhalb der (ab)-Ebene ein pseudo-Trägheitsdefekt berechnen:
Dc = 2(S(mi ci²) - Pc) . (25)Dies ist vor allem dann sinnvoll, wenn, wie im Fall der zu untersuchenden Moleküle, die Planarität eines Ringsystems untersucht werden soll, welches Substituenten trägt, die nicht in dieser Ebene liegen.
Eine weitere Bedingung, die oft zur Definition von Kreuzkonjugation angeführt wird, ist die, daß die beiden Doppelbindungen zwar in Konjugation zu einer dritten Doppelbindung stehen, jedoch nicht miteinander konjugiert sind. Das gilt zwar für das Methylenpentadien (VII), nicht jedoch für das cyclische Analogon Fulven (VI), das meist jedoch ebenfalls als kreuzkonjugierte Verbindung betrachtet wird.
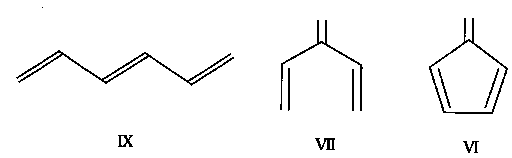 |
| Abb. B.2: Lineare Konjugation links und Kreuzkonjugation rechts. |
Einige Autoren weiten den Begriff der Kreuzkonjugation noch auf "ungesättigte Zentren" anstelle der Doppelbindungen aus. Solche "ungesättigten Zentren" können auch Heteroatome mit einsamen Elektronenpaaren wie Stickstoff oder Sauerstoff sein. In diesem Sinne sind dann auch Verbindungen wie Harnstoff kreuzkonjugiert.
In dieser Arbeit wird die erste (und gebräuchlichste) Definition verwendet. Unter einem kreuzkonjugierten System soll also ein System von drei Doppelbindungen verstanden werden, in dem zwei Doppelbindungen mit einer dritten, "zentralen" Doppelbindung konjugiert sind, so daß sich ein Y-förmiges p-Bindungssystem ausbildet. Ganz bewußt ausgeklammert werden hier Moleküle mit chinoiden Strukturen. Solche Gruppen spielen vor allem in der Farbstoffchemie eine wichtige Rolle. Obwohl man sie gewissermaßen als "doppelt" kreuzkonjugiert betrachten könnte, bilden sie doch eine vollkommen andere Substanzklasse. Sie unterscheiden sich in ihren elektronischen Eigenschaften deutlich von den kreuzkonjugierten Verbindungen und werden demzufolge in dieser Arbeit nicht behandelt.
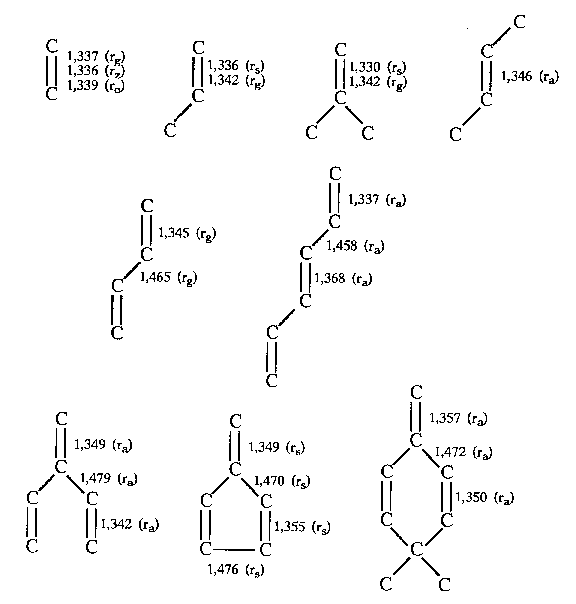 |
| Abb. B.3: Strukturdaten einigerKohlenwasserstoffe aus [22]. |
Der erste Referenzpunkt ist das Ethen. Die experimentellen Werte für die C=C-Bindungslänge im Ethen betragen je nach verwendeter Methode und je nach der Art des angegebenen Abstands 1,336 bis 1,339 Å. Insbesondere der rg-Abstand ist hierbei interessant, da viele der Vergleichswerte ebenfalls als rg-Abstände vorliegen. Er beträgt im Ethen 1,337 Å.
Wird nun an das Ethen gleichsam eine weitere Doppelbindung angefügt, so gelangt man zum (linear konjugierten) 1,3-Butadien. Dessen C=C-Abstand (ebenfalls rg) beträgt 1,345 Å. Die Bindung ist somit deutlich länger als die im Ethen. Es sollte jedoch auch bemerkt werden, daß im Propen, bei dem keine klassische Konjugation vorliegt, der (rg-)C=C-Abstand 1,342 Å beträgt, also
ebenfalls etwas länger ist als im Ethen. Hingegen wurde der rs-Abstand mit 1,336 Å bestimmt, d.h. effektiv gleich wie im Ethen. Hier zeigt sich, daß die Effekte der Konjugation auf die Bindungslänge mitunter so klein sind, daß sie bereits von experimentellen Ungenauigkeiten und/oder den prinzipiellen Schwierigkeiten bei der Strukturbestimmung überlagert oder gar gänzlich überdeckt werden können - ganz abgesehen von Effekten, die andere funktionelle Gruppen ausüben können. Noch drastischer wird der Effekt, wenn man die Daten für Isobuten (2-Methyl-Propen), einem Ethen mit zwei geminalen Methylgruppen, vergleicht. Hier beträgt der rs-Abstand sogar nur 1,330 Å, während der rg-Abstand wiederum mit 1,342 Å bestimmt wurde.
Eine weitere Doppelbindung kann an das Butadien auf zweierlei Weise "angefügt" werden. So erhält man entweder das linear konjugierte 1,3,5-Hexatrien (IX) oder das kreuzkonjugierte 3-Methylen-1,4-pentadien (VII). Im Hexatrien wurde die Länge (ra) der zentralen Doppelbindung, welche mit zwei anderen Doppelbindungen in Konjugation steht, zu 1,368 Å (trans) bzw. 1,362 Å (cis) bestimmt, was eine ganz erhebliche Verlängerung gegenüber dem Ethen darstellt. Für die beiden äußeren Doppelbindungen wurden Bindungslängen von 1,337 Å gefunden, was genau dem (rg-)Wert für das Ethen entspricht.
Beim kreuzkonjugierten Methylenpentadien ist die zentrale Methylen-Doppelbindung ebenfalls mit zwei Doppelbindungen konjugiert. Ihre Bindungslänge (ra) wurde jedoch zu 1,349 Å bestimmt, während als Bindungslänge für die äußeren Doppelbindungen ein (ra-)Wert von 1,342 Å gefunden wurde. Daraus kann man folgern, daß hier im wesentlichen zwei Butadien-Systeme vorliegen, die sich kaum gegenseitig beeinflussen.
Wie oben schon erwähnt, ist das Methylenpentadien nicht eben gebaut, weswegen die Konjugation gestört sein könnte. Aber auch beim planaren Fulven, welches das cyclische Analogon zum Methylenpentadien darstellt, finden sich ähnliche Verhältnisse: für die beiden Doppelbindungstypen wurden (rs-)Abstände von 1,349 Å (exocyclisch, entspricht der mittleren Doppelbindung) bzw. 1,355 Å (endocyclisch, entspricht den äußeren Doppelbindungen) gefunden. Das heißt, auch hier weicht die Bindungslänge der mittleren Bindung deutlich von dem Wert ab, der in der entsprechenden linear konjugierten Verbindung gefunden wird. Jedoch sind die Verhältnisse auch hier wiederum nur bedingt vergleichbar, da die beiden endocyclischen Doppelbindungen miteinander konjugiert sind, was im linearen Hexatrien nicht der Fall ist. Man sieht also, daß ein Vergleich zwischen verschiedenen Molekülen nur sehr schwierig möglich ist. Eine Übersicht, in die auch weitere Moleküle mit einbezogen sind, findet sich in Abb. B.3.
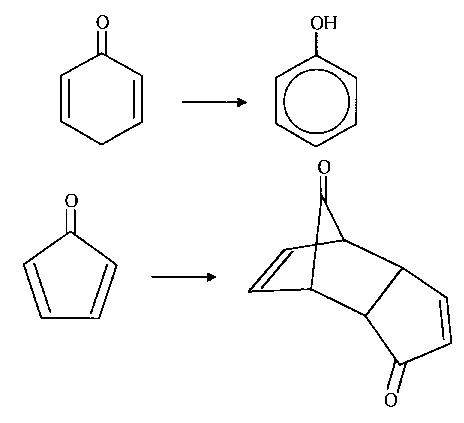 |
| Abb. B.4: "Spontane" Reaktionen
kreuzkonjugierter Verbindungen: Tautomerie des Cyclohexadienon/Phenol-Systems (oben) und Dimerisierung von Cyclopentadienon (unten). |
p-Bindungsordnung DE (eV)
Molekül AM1 HMO AM1 HMO
C=C 1,0 1,0 11,99 10,20
1
C=C 1 0,983 -
2\C 2 0,177 - 11,36 -
1 /C
C=C 1 0,970 -
2\C 2 0,169 - 10,83 -
1
C=C 1 0,963 0,894
2\C=C 2 0,269 0,447 9,78 6,32
1
C=C 3 1 0,958 0,871
2\C=C 2 0,284 0,483 8,83 4,59
\C=C 3 0,921 0,785
1 /C=C 1 0,929 0,816
C=C 3 2 0,262 0,408 9,17 5,30
2\C=C 3 0,964 0,908
1 /C=C 1 0,929 0,759
C=C |4 2 0,261 0,449
2\C=C 3 0,920 0,778 9,50 4,44
3 4 0,308 0,520
Tab. B.3: p-Bindungsordnungen und Anregungsenergien einiger ungesättigter Kohlenwasserstoffe,
Für Ethen sind die p-Bindungsordnungen bei beiden Methoden erwartungsgemäß genau 1,0 und auch die DE-Werte* stimmen mit 10,20 eV (HMO) bzw. 11,99 eV (AM1) noch gut überein. Für Butadien treten dagegen bereits deutliche Unterschiede auf. Hier beträgt DE(HMO) nur 6,32 eV, während DE mit der AM1-Methode zu 9,78 eV berechnet wird. Das Verhältnis der Energieunterschiede von Ethen und Butadien sollte auch grob dem reziproken Verhältnis der längstwelligen UV-Absorption (p-p*-Übergang) der Moleküle entsprechen. Die entsprechenden Wellenlängen sind für Ethen 190 nm und für Butadien 217 nm [24]. Es ergibt sich daraus ein Verhältnis von 1,14. Das Verhältnis der HOMO-LUMO Energieunterschiede von Ethen und Butadien ist für AM1 1,23, für die HMOMethode jedoch 1,61. Das semi-empirische Verfahren scheint die physikalische Wirklichkeit also deutlich besser zu beschreiben als das einfache HMO-Modell.
* Die Energieunterschiede ergeben sich aus den HMO-Rechnungen in Einheiten des Resonanzintegrals b, für das in [3] ein Wert von 5,1 eV angegeben wird,
Auch in den p-Bindungsordnungen zeigen sich deutliche Unterschiede zwischen den beiden Methoden. Während AM1 für Butadien fast dieselben Werte (p-Bindungsordnung der Doppelbindungen: 0,96) wie für Propen oder Isobuten liefert*, in denen keine klassische Konjugation vorliegt, - und damit kaum eine Veränderung gegenüber dem Ethen festzustellen ist - bewertet das HMO-Verfahren die Konjugation deutlich höher (p-Bindungsordnung der Doppelbindungen: 0,89). Dieser Trend setzt sich auch beim nächsten linear konjugierten Glied der Polyen-Kette, dem Hexatrien (IX), fort. Die mit AM1 berechneten Werte ändern sich kaum (p-Bindungsordnung der mittleren Doppelbindung: 0,92), während die HMO-Methode einen deutlich stärkeren konjugativen Effekt vorhersagt (p-Bindungsordnung der mittleren Doppelbindung: 0,79).
* Diese Moleküle können mit dem einfachen HMO-Verfahren nicht berechnet werden, da die Methylgruppen keine einfach besetzten p-Orbitale besitzen.
Dementsprechend verschieden fallen auch die Unterschiede zwischen dem linear konjugierten Hexatrien (IX) und dem kreuzkonjugierten Methylenpentadien (VII) aus. Während mit AM1 kaum ein Effekt zu sehen ist ändern sich die mit dem HMO-Verfahren berechneten Bindungsordnungen drastisch. Auch in den HOMO-LUMO-Energiedifferenzen unterscheiden sich die kreuzkonjugierten Kohlenwasserstoffe nicht auffällig von den linear konjugierten Verbindungen. Ein systematischer elektronischer Effekt ist auf diese Weise also nicht nachweisbar.
 Zurück zum Inhaltsverzeichnis
Zurück zum Inhaltsverzeichnis